Todos los que hemos estudiado contabilidad conocemos a Fray Luca Pacioli, fraile franciscano italiano del s. XV a quien debemos el sistema contable de partida doble (el debe y el haber) que desde entonces se ha utilizado en todas las instituciones y compañías mercantiles…
Pero este monje no solo desarrolló la moderna contabilidad, sino que aportó obras tan importantes como la Divina Proporción, manuales de matemáticas y manuales de Ajedrez.
Entre todas sus aportaciones, queremos aquí destacar una muy importante, denominada “la regla del 72”. Se trata de un método de resolución de problemas financieros que se aproximó a los logaritmos casi un siglo antes de que Jhon Napier desarrollase la logarítmica.
Qué es la regla del 72 y para qué sirve
Esta regla del 72 nos permite de forma muy sencilla calcular cuántos años necesitamos para duplicar nuestra inversión, o bien dado un plazo de años determinado a qué tipo de interés se tendría que reinvertir para duplicar la inversión.
Primero recordemos que nuestra inversión se puede capitalizar a interés simple o bien a interés compuesto.
Diferencia interés simple VS interés compuesto
El interés simple significa que los intereses se cobran por el inversor y no se reinvierten, por lo que la fórmula matemática para calcular el rendimiento sería
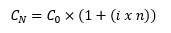
Donde Cn es el capital final obtenido, Co es el capital inicial invertido, “i” es el tipo de interés que se cobra, y “n” es el término temporal en el que se cobran intereses por dicha inversión.
Como vemos, calcular aquí cuánto se tardaría en duplicar la inversión es relativamente sencillo, dado que basta con realizar operaciones aritméticas simples.
Sin embargo, el interés compuesto implica que los intereses generados por la inversión se reinvierten al mismo tipo de interés. Así, la fórmula matemática sería como sigue:
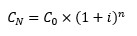
En este caso, el factor tiempo actúa como exponente, puesto que los nuevos intereses generados cada cierto tiempo se añaden a la inversión inicial. Por eso, con interés compuesto, calcular el plazo necesario para duplicar la inversión requeriría operaciones complejas que hoy resolveríamos con logaritmos.
Para qué sirve la regla del 72
Fray Luca Pacioli nos dio la regla simple para calcular aritméticamente el plazo de tiempo necesario para multiplicar por dos lo invertido.
1.Calcula el tiempo que necesitas para duplicar tu dinero
Basta con dividir 72 entre el tipo de interés (multiplicado por 100) y obtendremos el tiempo necesario para duplicar nuestra inversión.
[EJEMPLO 1]
Veamos cómo funciona con un ejemplo. Pensemos que invertimos 10.000 € a un tipo de interés compuesto anual del 4 %. Cada año aplicando la fórmula del interés compuesto ganamos 400 € por lo que el capital final tras la inversión de un año será de 10.400 €.
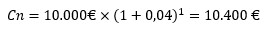
Con la regla del 72 podemos calcular de forma rápida el número de años necesario para que este capital final de nuestro ejemplo sea al menos de 20.000 €. Habiendo duplicado con el tiempo la inversión inicial.
Procedemos a dividir 72 entre el tipo de interés en términos absolutos, es decir, entre 4, y obtenemos como resultado 18 años. Veamos cómo efectivamente el resultado es aproximadamente correcto.
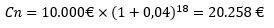
Si probamos con cualquier otro tipo de interés, veremos que el número de años calculado siempre permite duplicar la inversión según el tipo de interés compuesto utilizado.
2. Calcular el tipo de interés necesario para duplicar la inversión en un tiempo determinado
A la inversa, si tenemos un capital y un plazo de tiempo durante el cual podremos invertirlo, podemos calcular el tipo de interés compuesto al cual lo debemos invertir para duplicar la inversión.
[EJEMPLO 2]
Sería tan sencillo como:
Dividir 72 entre el número de años
¿Qué significa el resultado? El valor en términos absolutos del tipo de interés a requerir para multiplicar la inversión por dos en el plazo de años que tendremos disponible el capital.
Por ejemplo, si durante 10 años que nos faltan para la jubilación vamos a disponer de 30.000€ ahorrados, ¿qué tipo de interés deberíamos requerir para duplicar este capital en el momento de jubilarnos?
Al dividir 72 entre 10 obtenemos 7,2 por lo que el interés que duplica esta inversión en 10 años es de 7,2%.
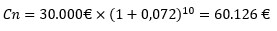
Conclusión: por qué usar la regla del 72
¿Cómo es posible que esta regla tan sencilla funcione?
Porque si calculamos a qué exponente es necesario elevar la suma del tipo de interés porcentual más 1 para que el resultado sea 2, dicho exponente necesario será igual al resultado de la fracción entre 72 y el tipo de interés (este último multiplicado por 100, no en términos porcentuales).
Este cálculo corresponde en las matemáticas modernas al campo de los logaritmos y del cálculo infinitesimal, pero el conocimiento de Fray Luca Pacioli nos lo brindó en forma de sencilla regla financiera hace ya cinco siglos.







































